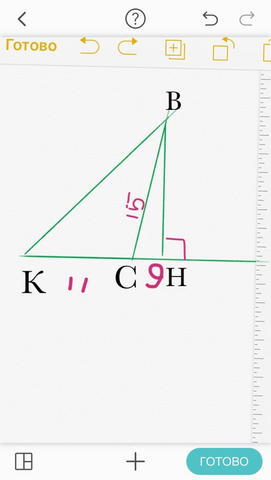
Начертим правильно рисунок.
Треугольник ВКС.
Высота ВН лежит вне треугольника.
Точка Н находится на продолжении стороны КС.
Отмечаем на рисунке ВС=15
СН=9
КС=11
ВН-высота, следовательно, треугольник ВНС - прямоугольный.
Нам известны гипотенуза 15 и катет 9.
По теореме Пифагора
ВН=корень из (225-81)= 12
Рассмотрим треугольник ВКС.
Площадь = высота*основание*0,5=ВН*КС*0,5=12*11*0,5=66.
Ответ: 66