V pryamougolnom treugolnike bisectrisa pryamogo ugla delit gipotenuzu na otrezki dlinnoy...

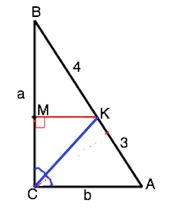
В прямоугольном треугольнике биссектриса прямого угла делит гипотенузу на отрезки длиной 3 и 4. Найти катеты треугольника и эту биссектрису.

------------

Обозначим треугольник АВС, угол С=90°, СК - биссектриса.

Примем ВС=а. АС=b.

Биссектриса внутреннего угла треугольника делит противолежащую

сторону на части, пропорциональные прилежащим сторонам. ⇒

AB:BC=AK:BK=3/4 ⇒

b:a=3:4.

3a=4b ⇒ b=3a/4

По т.Пифагора

АВ²=а²+b²

49== a²+9a/16= 25a²/16 ⇒

a²=49•16/25 ⇒

a=5,6 ( катет ВС)

b=5,6•3/4=4,2 (катет АС)

Проведем КМ║АС.

Прямоугольный ∆ КВМ~∆ АВС по общему острому углу B, k=BK:AB=4/7 ⇒

MK :АС=4/7

MK=4,2•4/7=2,4

В прямоугольном ∆ СМК угол МСК=45° ⇒

$CK= \frac{MK}{sin45 ^{o} } = \frac{2,4}{ \frac{ \sqrt{2} }{2} } =2,4 \sqrt{2}$ ед. длины

—————

Для нахождения биссектрисы можно воспользоваться т.косинусов, но там неудобные вычисления с √2.