Стороны треугольника a=13, b=14, c=15. из них двое (а и b) являются касательными к...

Question

Стороны треугольника a=13, b=14, c=15. из них двое (а и b) являются касательными к окружности центр которой лежит на третьей стороне. Найдите радиус окружности.

Answer 1

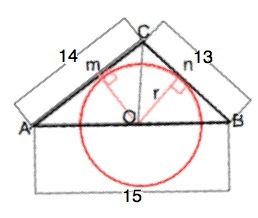
Обозначим вершины данного треугольника АВС, центр окружности - О. 

Соединим С и О. 

Проведем в точки касания окружности радиусы  Om и On.  

Радиус, проведенный в точку касания, перпендикулярен касательной. 

Следовательно, Om и On  - высоты  треугольников АОС и ВОС. 

S ACB=S ∆ AOC+S ∆ BOC=r•(AC+BC):2 

r=2 S ∆ ACB:(14+13)

По формуле Герона  S ∆ ACB=84 (можно проверить, сделав нужные вычисления самостоятельно).   

---