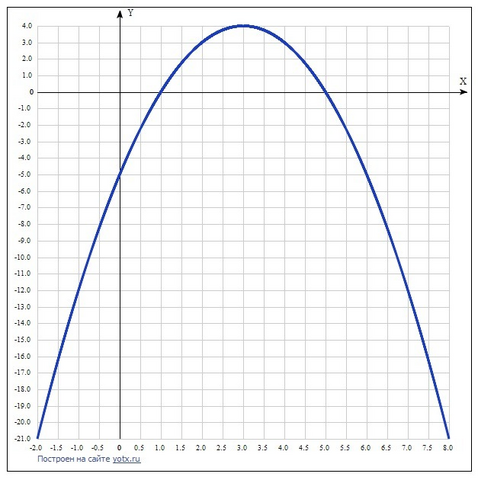
Дана функция y=-x^2 + 6x - 5.
График этой функции - парабола ветвями вниз.
Вершина параболы Хо = -в/2а = -6/-2 = 3,
Уо = -9+18-5 = 4.
Точки пересечения оси Ох:
-х² + 6х - 5 = 0,
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=6^2-4*(-1)*(-5)=36-4*(-1)*(-5)=36-(-4)*(-5)=36-(-4*(-5))=36-(-(-4*5))=36-(-(-20))=36-20=16;Дискриминант больше 0, уравнение имеет 2 корня:
x₁=(√16-6)/(2*(-1))=(4-6)/(2*(-1))=-2/(2*(-1))=-2/(-2)=-(-2/2)=-(-1)=1;x₂=(-√16-6)/(2*(-1))=(-4-6)/(2*(-1))=-10/(2*(-1))=-10/(-2)=-(-10/2)=-(-5)=5.Точка пересечения оси Оу берётся из уравнения при х = 0, у = -5.
По графику (и по анализу) определяем:
1) промежуток убывания функции: х ∈ (3; ∞);
2) при каких значениях x функция принимает отрицательные значения:
х ∈ (-∞; 1) ∪ (5; +∞).