В равнобедренный треугольник один угол которого равен 120° вписана окружность радиуса R....

В равнобедренный треугольник один угол которого равен 120°, вписана окружность радиуса R. Найдите основание треугольника.

* * *

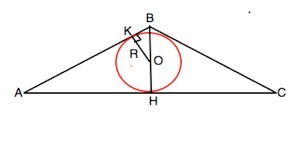
Обозначим треугольник АВС, угол АВС=120°; высота - ВН, центр окружности – О, ОК - радиус, проведенный в точку касания с боковой стороной. .

По свойству равнобедренного треугольника его высота ещё биссектриса и медиана.⇒ ∠АВН=∠СВН=120°:2=60° и АС=2АН.

∆ ОКВ – прямоугольный.

ВО=R:sin 60°=2R:√3

$BH=BO+OH= \frac{2R}{ \sqrt{3}} +R= \frac{R*(2+ \sqrt{3)} }{ \sqrt{3}}$

$AH= \frac{BH}{ctg 60^{o}}= \frac{R(2+ \sqrt{3}) }{ \sqrt{3}} : \frac{1}{ \sqrt{3}} =R(2+ \sqrt{3} ) \\ AC=2AH=2R(2+ \sqrt{3} )$

АС=2R(2+√3)