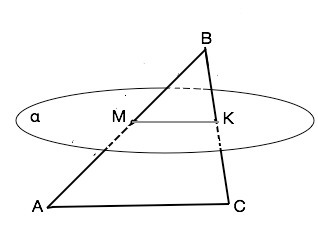
Если в одной из пересекающихся плоскостей лежит прямая, параллельная другой плоскости, то она параллельна линии пересечения плоскостей. (свойство)
Плоскость α параллельна АС, следовательно, МК, линия пересечения плоскостей АВС и α, параллельна АС.
В ∆ АВС МК║АС. Поэтому соответственные ∠ВМК и ∠ВАС равны, угол В общий для треугольников АВС и МВК, ⇒ эти треугольники подобны.
Примем коэффициент подобия равным а.
ВК:СК=ВМ:МА=3а:4а, ⇒ВС=ВК+СК=7а.
k=ВС:ВК=7:3 - (доказано).
Отсюда АС:МК=7:3
14:МК=7:3 ⇒ 7МК=42,
МК=6 см