Точка Q лежит ** медиане CM треугольника ABC. Если CQ=2QM и площадь ABC равна 144, то...

Question

Точка Q лежит на медиане CM треугольника ABC. Если CQ=2QM и площадь ABC равна 144, то чему равна площадь AQM?

Answer 1

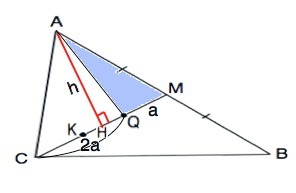
Медиана треугольника делит его на два равновеликих, т.е. равных по площади. 

Рассмотрим ∆ АСМ. Его площадь равна половине площади ∆ АВС, т.е. 72 (ед. площади). 

Точка Q делит СМ в отношении QM:MC=1:2

Высота АН - общая для треугольников АСМ, АСQ и АМQ.

Площади треугольников с равными высотами относятся как длины их оснований. S (∆MAQ):S(∆ACM)=СQ:CM=1/3 ⇒

S (∆ AQM)=S (∆ ACM):3=24 (ед. площади)

---