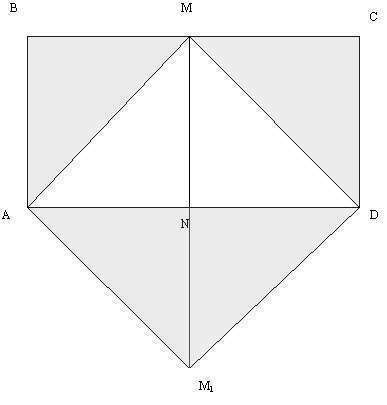
Углы А и D прямые, значит, ∠MAD = ∠MDA = 45°, т.к. AM и DM биссектрисы этих углов. Тогда треугольник ΔAMD равнобедренный и AM = DM = 5 см.
Из точки М опустим перпендикуляр MN на сторону АD. Углы ∠BMA = ∠AMN = 45°.
Треугольники ΔABM = ΔAMN по общей стороне и двум углам, прилегающим к ней. Аналогично, равны ΔMCD = ΔMDN.
Как видим на рисунке, прямоугольник ABCD превращается в квадрат AMDM1 со стороной 5 см. Следовательно, его площадь равна 25 см².
Ответ: 25