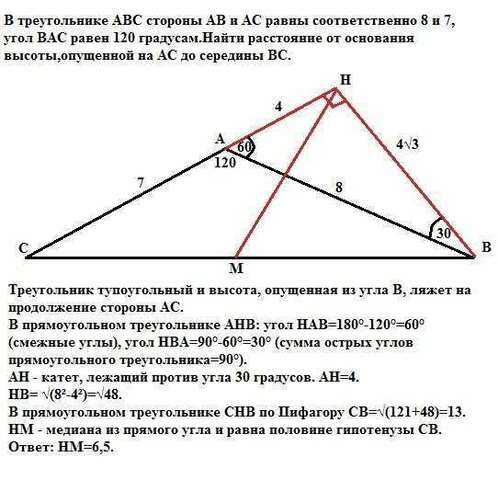
Треугольник тупоугольный и высота, опущенная из угла В, ляжет на продолжение стороны АС.
В прямоугольном треугольнике АНВ: угол НАВ=180°-120°=60° (смежные углы), угол НВА=90°-60°=30° (сумма острых углов прямоугольного треугольника=90°).
АН - катет, лежащий против угла 30 градусов. АН=4.
НВ= √(8²-4²)=√48.
В прямоугольном треугольнике СНВ по Пифагору СВ=√(121+48)=13.
НМ - медиана из прямого угла и равна половине гипотенузы СВ.
Ответ: НМ=6,5.