В сегмент окружности образованный хордой в 6 см вписан квадрат со стороной 2 см. Найдите...

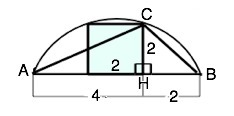
Обозначим хорду АВ, вершины квадрата, лежащие на окружности, СD, соединим эти точки последовательно. DC||АВ, АВСD- трапеция. Вписать в окружность можно только равнобедренную трапецию. Опустим из С высоту СН и проведем диагональ АС.
Высота равнобедренной трапеции, опущенная из вершины тупого угла на большее основание. делит его на два отрезка, из которых меньший равен полуразности, больший – полусумме оснований.
ВН=2, АН=4
Треугольник АСВ вписан в тот же сегмент, что и квадрат, его высота СН – сторона квадрата и равна 2 см.
Радиус описанной около треугольника окружности находят по формуле R=a•b•c:4S, т.е. он равен произведению сторон треугольника, деленному на его учетверенную площадь
По т.Пифагора АС=√(AH²+CH²)=√(16+4)=2√5
По т.Пифагора ВС=√(CH²+BH²)=√8=2√2
S (АВС)=СН•AB:2=2•6:2=6 (см²)
a•b•c=6•2√5•2√2=24√10
4S=24
R=24√10:24=√10 (см)
Или,
используя найденные выше значения АС и ВС:
$sin(CAB)= \frac{CH}{AC} = \frac{2}{2 \sqrt{5} }$
$sin(CAB)= \frac{1}{ \sqrt{5}}$
По т.синусов
$2R= \frac{CB}{sin(CAB)} = \frac{2 \sqrt{2} }{ \frac{1}{ \sqrt{5} } } =2 \sqrt{10} \\ R= \sqrt{10}$ см