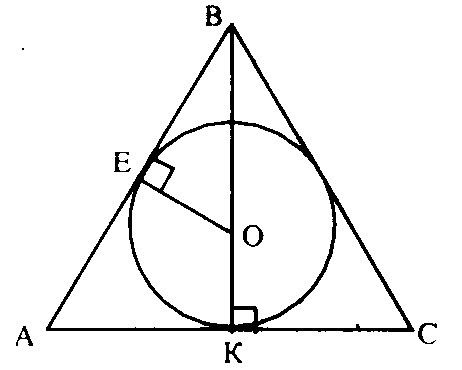
ABC - равнобедренный треугольник с основанием AC, боковыми сторонами AB=BC.
Точка касания окружности делит сторону AB на отрезки: AE=5cм, BE=6cм ⇒ AB = AE + BE = 5 + 6 = 11 (см) ⇒ BC = 11 cм
Опустим высоту BK на основание AC.
AE = AK (свойство касательных) ⇒ AK = 5 cм ⇒ AC = 2*AK = 2*5 = 10(см), т.к. BK является высотой, медианой и биссектрисой, проведенной к основанию равнобедеренного треугольника.
Периметр треугольника - сумма длин всех сторон
P = AB + BC + AC
P = 11 + 11 + 10 = 32 (cм)
Ответ Г