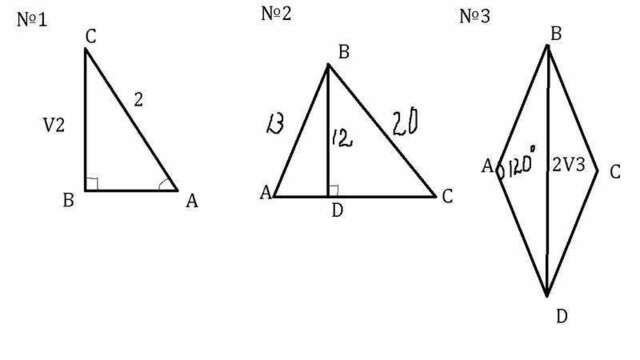
№3
Пусть весь ромб ABCD
∠A=∠C=120° ⇒
∠B=∠D=180-120=60°
Рассмотрим треугольник ABD, ∠А=120°, BD=2√3, AB=AD
BD=√(AB²+AD²-2AB*ADcosA)
BD²=AB²+AB²-2AB²cos60°
(2√3)²=2AB²+2*1/2*AB²
3AB²=12
AB²=4
AB=2 см сторона ромба
Поскольку все стороны ромба равны
Р=4АВ=4*2=8 см периметр
№1
Найдем синус острого угла - это отношение противолежащего катета к гипотенузе
sin A=BC/AC=√2/2 ⇒
∠A=45°, а значит ∠A=∠C=45° и треугольник равнобедренный, а значит второй катет АВ=√2
№2
Рассмотрим треугольник BDC - прямоугольный, поскольку BD - высота.
По теореме пифагора:
DC²=BC²-BD²
DC²=20²-12²
DC²=400-144
DC²=256
Dc=16 cм
Треугольник ABD - прямоугольный, поскольку BD - высота.
По теореме пифагора:
AD²=AB²-BD²
AD²=13²-12²
AD²=169-144
AD²=25
AD=5 см
АС=AD+DC=5+16=21 см
РΔ=AB+AC+BC=21+20+13=54 См
Ответ 54 см