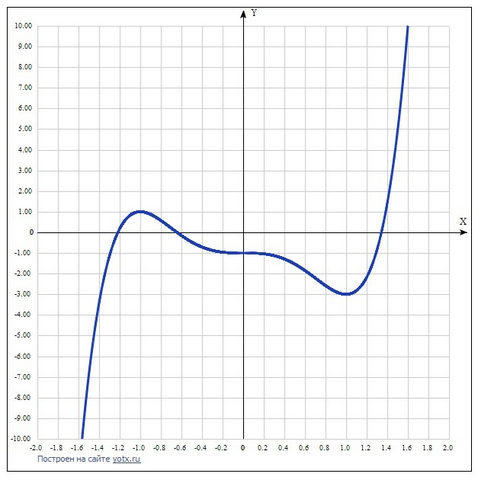
Дана функция f (x)= 3x⁵ - 5x³ - 1 .
1) Производная равна y' = 15x⁴ - 15x².
Приравняем её нулю: 15x⁴ - 15x² = 0.
15x²(x² - 1) = 0.
Отсюда имеем 3 критические точки:
х = 0,
х = 1,
х = -1.
Находим значения производной вблизи этих точек.
x =
-2
-1
-0,5 0 0,5
1 2
y' =
180
0 -2,8125 0
-2,8125
0 180.
Как видим, имеем 2 точки экстремума:
х = -1 точка локального максимума (производная меняет знак с + на -).
х = 1 точка локального минимума (производная меняет знак с - на +).
2) Промежутки возрастания и убывания находим по знаку производной.
Где
производная положительна - функция возрастает, где отрицательна - там убывает.
Возрастает: х = (-∞; -1) ∪ (1; +∞).
Убывает: х = (-1; 1).
3) В точке х = 0 у = -1, в точке х = 1 минимум, у = -3 это наименьшее значение функции на отрезке [0; 2].
Так как функция возрастает при х > 1, то наибольшее значение функции на [ 0 ; 2 ]:x =
2,
y =
55.