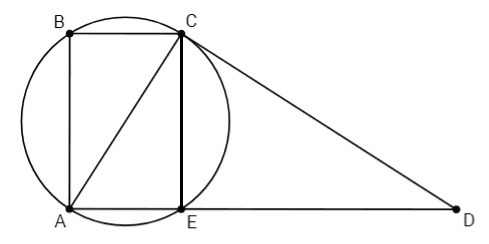
∠ABC =90, ∠CEA =90 (вписанный угол, опирающийся на диаметр)
∠DAB =90 (односторонний с ∠AВC при параллельных основаниях трапеции)
ABCE - прямоугольник =>
AB=СЕ
AE=BC
DE= √(CD^2-CE^2) = √(CD^2-AB^2) =√(100*13-25*3)=35
∠ACD =90 (угол между радиусом и касательной)
∠ECD=90-∠ACE
∠BCA=90-∠ACE
∠ECD=∠BCA
△ECD~△BCA
BC/CE=AB/DE <=> BC=AB^2/DE <=> BC=15/7 (2,1428)
SABCD= (AE+DE+BC)*AB/2 =(2BC+DE)*AB/2 =1375*√3/14 (170,11)