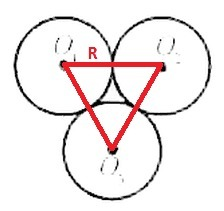
Отрезок, соединяющий центры касающихся окружностей, проходит через точку их касания (радиусы касающихся окружностей, проведенные в точку касания, перпендикулярны касательной и образуют развернутый угол).
Треугольник O₁O₂O₃ - равносторонний со стороной 2R.
Площадь равностороннего треугольника: S= a^2 *√3/4
S(O₁O₂O₃)= (2R)^2 *√3/4 = R^2 *√3
Все углы равностороннего треугольника равны 60°.
Площадь сектора: S= πr^2 *α/360°
Sсек= πR^2 60°/360° = πR^2/6
Искомая площадь - разность площадей равностороннего треугольника со стороной 2R и трех секторов с углом 60° и радиусом R.
S= S(O₁O₂O₃) -3*Sсек = R^2 *√3 -3πR^2/6 = R^2(√3 -π/2)