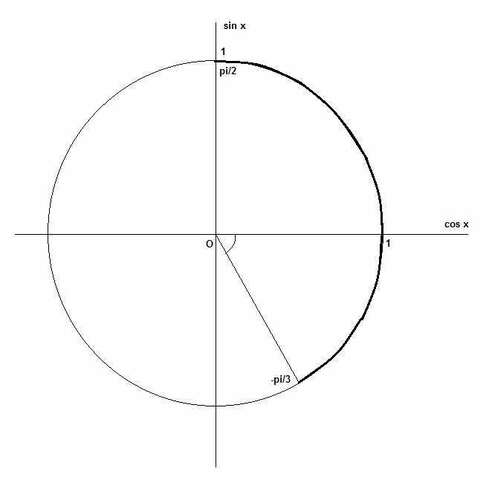
; x ∈ [-pi/3; pi/2]


Знаменатель - сумма квадратов и 1, он больше 0 при любых x и а.
Значит, числитель меньше 0.
-a^2 + a + 3 - (1 - cos^2 x) - cos x*(a^2-2a+0,5) < 0
cos^2 x - cos x*(a^2-2a+0,5) - (a^2-a-2) < 0
Квадратное неравенство относительно cos x.
D = (a^2-2a+0,5)^2 + 4(a^2-a-2) = a^4-4a^3+a^2-2a+0,25+4a^2-4a-8 =
= a^4-4a^3+5a^2-6a-7,75 >= 0
Решение этого неравенства: a ∈ (-oo; -0,6742) U (3,255; +oo)
cos x1 = (-a^2+2a-0,5 - √(a^4-4a^3+5a^2-6a-7,75) )/2
cos x2 = (-a^2+2a-0,5 + √(a^4-4a^3+5a^2-6a-7,75) )/2
Эти два решения должны попадать в промежуток [-pi/3; pi/2], поэтому
x1 = +arccos [(-a^2+2a-0,5 - √(a^4-4a^3+5a^2-6a-7,75) )/2] ∈ [0; pi/2]
x2 = -arccos [(-a^2+2a-0,5 - √(a^4-4a^3+5a^2-6a-7,75) )/2] ∈ [-pi/3; 0]
x3 = +arccos [(-a^2+2a-0,5 + √(a^4-4a^3+5a^2-6a-7,75) )/2] ∈ [0; pi/2]
x4 = -arccos [(-a^2+2a-0,5 + √(a^4-4a^3+5a^2-6a-7,75) )/2] ∈ [-pi/3; 0]
Осталось решить эти промежутки, но у меня на это уже сил нет.
На рисунке я показал, куда попадают эти корни.
x1 и x3 - положительные, они находятся в 1 четверти.
x2 и x4 - отрицательные, они находятся в 4 четверти.