Высота к AC по формуле Герона:
p= (AB+BC+AC)/2 =18
H= 2√[p(p-AB)(p-BC)(p-AC)]/AC =
= 2√(18*6*8*4)/14 = 24√6/7
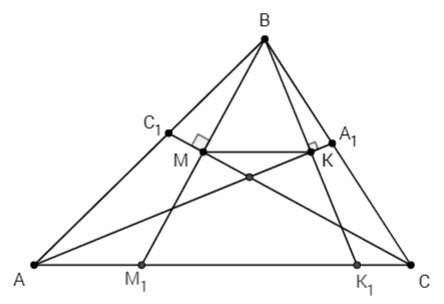
В треугольниках BAK1, BCM1 биссектриса является высотой => т. равнобедренные.
CB=CM1
AB=AK1
M1K1= AC-(AC-AK1)-(AC-CM1) = AB+CB-AC = 8
SBK1M1= M1K1*H /2 =4*24√6/7
В равнобедренных т. биссектриса является также медианой => MK соединяет середины BM1 и BK1 => MK - средняя линия BK1M1.
Площадь треугольника, отсекаемого средней линией, равна 1/4 площади исходного.
SBKM = SBK1M1 /4 = 24√6/7 (~8,4)