Рассматриваем первое уравнение. Раскрываем модули:
1) x >= 5y - 5
x^2 + 5x + y^2 - y - x + 5y - 5 = 52
x^2 + 4x + 4 + y^2 + 4y + 4 = 65
(x + 2)^2 + (y + 2)^2 = 65 - это уравнение окружности с центром в точке (-2, -2) и радиусом корень из 65.
2) x < 5y - 5:
x^2 + 5x + y^2 - y + x - 5y + 5 = 52
x^2 + 6x + 9 + y^2 - 6y + 9 = 65
(x + 3)^2 + (y - 3)^2 = 65 - это уравнение окружности с центром в точке (-3, 3) и радиусом корень из 65.
чтобы было проще рисовать, найдем координаты пересечения окружностей:
x - 5y + 5 = 0 -> x = 5y - 5
(5y - 5)^2 + 5(5y - 5) + y^2 - y = 52
25y^2 - 50y + 25 + 25y - 25 + y^2 - y = 52
26y^2 - 26y - 52 = 0
y^2 - y - 2 = 0
y = 2, x = 5 или y = -1, x = -10.
Второе уравнение:
y = 2 + a(x - 5) - общее уравнение всех невертикальных прямых, проходящих через точку (5, 2), у которых угловой коэффициент равен a.
Заметим, что точка (5, 2) - решение системы.
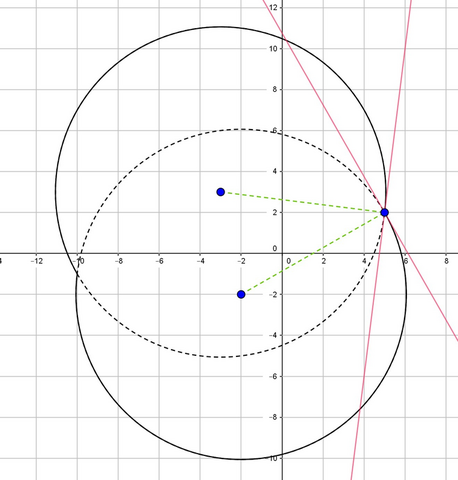
Изображаем решение первого уравнения на рисунке. Чтобы прямая, проходящая через (5, 2), пересекала график еще в одной точке, она не должна попасть в область между касательными к окружностям.
Угловые коэффициенты найдем из того, что радиус, проведенный к точке касания, перпендикулярен касательной, а также вспомнив, что если прямая с угловым коэффициентом k' перпендикулярная к прямой с угловым коэффициентом k, то k' = -1/k.
"Верхний" радиус соединяет точки (-3, 3) и (5, 2); угловой коэффициент (3 - 2)/(-3 - 5) = -1/8; угловой коэффииент касательной 8.
"Нижний" радиус: точки (-2, -2) и (5, 2); угловой коэффициент (2 - (-2))/(5 - (-2)) = 4/7; угловой коэффициент касательной -7/4.
Ответ. Система имеет не более двух решений при -7/4 <= a <= 8.<hr>