Найти:
1) Промежутки монотонности, наибольшее и наименьшее значение
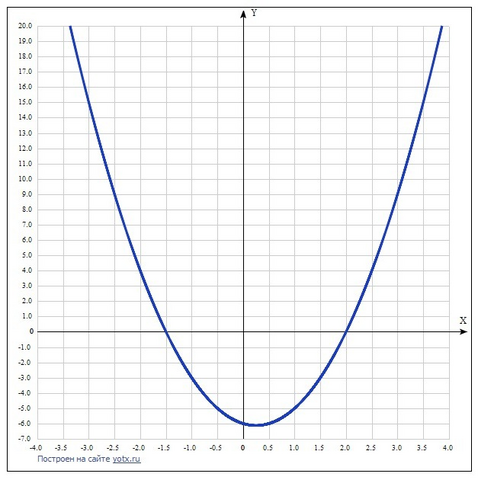
функции y=2x^2-x-6 на промежутке [-1;3]
;
График этой функции - парабола ветвями вверх.
Надо найти её вершину Хо = -в/2а = 1/4.
Уо = 2*(1/16)-(1/4)-6 = -98/16 = -6(1/8). Это минимальное значение.
Максимум - ∞.
Промежутки выпуклости функции y=2x^2-x-6 на промежутке [-1;3].
У параболы выпуклость только одна - в сторону вершины.
Для данной - выпуклость вниз.
2) Промежутки монотонности, наибольшее и наименьшее значение;
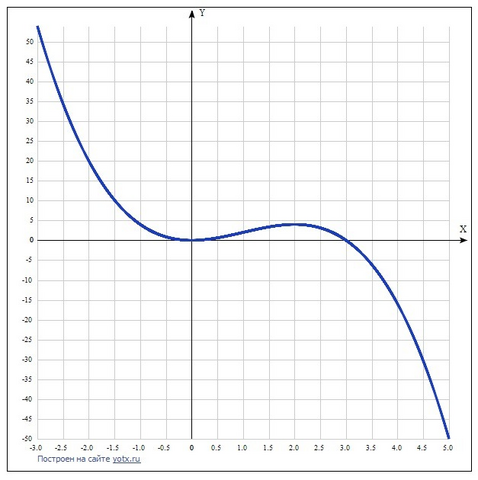
функции y=3x^2-x^3 на промежутке [-1;1].
Находим производную функции: y' = -3x² + 6x и приравняем её нулю:
-3х(х-2) = 0.
Имеем 2 критические точки: х = 0 и х = 2.
Это точки определяют 3 промежутка знака производной функции.
Где производная положительна - там функция возрастающая, где отрицательна - там функция убывающая.
x =
-1 0
1 2
3
y' = -3x² + 6x
-9
0
3
0
-9.
Функция возрастающая: х ∈ (-∞; 0) ∪ (2; +∞).
Функция убывающая: х ∈ (0; 2).
Промежутки выпуклости функции y=3x^2-x^3 на промежутке [-1;1].
Находим вторую производную y'' = -6x + 6.
-6(x - 1) = 0.
Точка перегиба х = 1.
х = 0 2
y'' = 6 -6.
Функция выпукла вниз: х ∈ (-∞; 1).
Функция выпукла вверх: х ∈ (1; +∞).