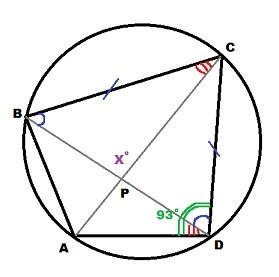
ВС = СD ⇒ ΔBCD - равнобедренный ⇒ ∠CBD = ∠CDB
∠BDA = ∠BCA опираются на одну дугу ∪BA ⇒
∠CBD + ∠BCA = ∠CDB + ∠BDA = ∠ADC = 93° ⇒
В треугольнике ΔBCP :
∠BPC = 180° - (∠CBP + ∠BCP) = 180°-93° = 87° < 90° ⇒ острый
Ответ: диагонали пересекаются под острым углом 87°