Помогите , пожалуйста, решить: Изобразить график функции заданной формулы и указать...

Упростим функцию:
$y= \sqrt{ (\frac{1}{3- \sqrt{5}}- \frac{1}{3+ \sqrt{5}})* \frac{ \sqrt{5}+ \sqrt{45}}{10}}*x^2+2= \\ =\sqrt{ \frac{3+ \sqrt{5}-3+ \sqrt{5}}{9-5}* \frac{ \sqrt{5}+3 \sqrt{5}}{10}}*x^2+2= \\ = \sqrt{ \frac{2 \sqrt{5} }{4}* \frac{4 \sqrt{5} }{10}}*x^2+2= \sqrt{ \frac{40}{40}}*x^2+2= \sqrt{1}*x^2+2=x^2+2.$
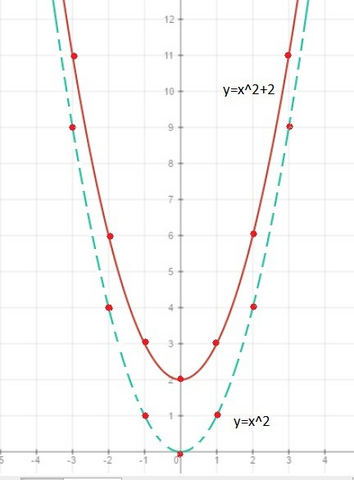
y=x²+2 - квадратичная парабола, которую можно построить путем сдвига функции у=х² на две единицы вверх вдоль оси OY.
у=х²:
х -3 -2 -1 0 1 2 3
у 9 4 1 0 1 4 9
у=х²+2:
х -3 -2 -1 0 1 2 3
у 11 6 3 2 3 6 11
График см. на рисунке.

Свойства:
1) Область определения: D=R.
2) Область значений: Е=[2;+∞).
3) Значение у=2 является наименьшим, наибольшего нет.
4) Функция чётная.
5) Функция непериодическая.
6) Точек пересечения с осью ОХ нет, т.е. нулей не имеет.
7) Точка пересечения с осью OY (0;2).
8) На промежутке (-∞;0] функция убывает, на промежутке [0;+∞) функция возрастает.
9) На всей области определения, т.е. на R функция принимает положительные значения.