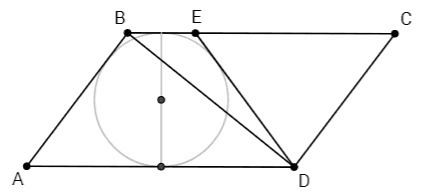
1) Если трапеция ABED равнобедренная (AB=ED) и в нее можно вписать окружность (сумма её оснований равна сумме боковых сторон), то выполняется равенство:
2AB=BE+AD <=> BE= 2AB-AD = 2*5-8 =2
2) Радиус вписанной в трапецию окружности равен половине высоты.
r= 4/2 =2
Sкр= пr^2 =4п (~12,56)
3) Диагональ равнобедренной трапеции ABED является также диагональю параллелограмма ABCD.
Для равнобедренной трапеции:
BD= √(AD*BE +AB^2) = √(8*2 +5^2) =√41 (~6,4)
(Для любой трапеции: сумма квадратов диагоналей равна сумме удвоенного произведения оснований и квадратов боковых сторон.)
Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов смежных сторон.
AC^2 +BD^2 = 2(AB^2 +AD^2) <=> AC= √(2(AB^2 +AD^2)-BD^2) = √(2(5^2 +8^2)-41) =√137 (~11,7)
4) SABCD= AD*h = 8*4 =32
SABCD= AC*BD*sin(a)/2 <=> sin(a)= 2*SABCD/AC*BD = 2*32/√(137*41) = 0,8539
acrsin(0,8539) =58,64