1)Периметр равностороннего треугольника равен 15,6 см, значит его стороны равны 15,6см: 3= 5,2 см. Боковая линия треугольника по опрелелению: пересекает две его стороны пополам, параллельна третьей и равна её половина, значит средняя линия равна 5,2см: 2= 2,6см
2) Пусть меньший угол равен х, тогда больший угол равен (х+20), всего сумма односторонних углов равна 180°, то:
2х+ 20= 180
2х=160
х= 80
Итак, один угол равен 80°
2)80°+ 20°= 100°
Ответ: 80°, 100°
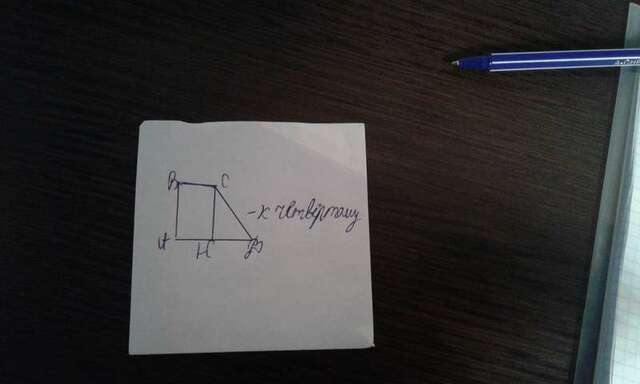
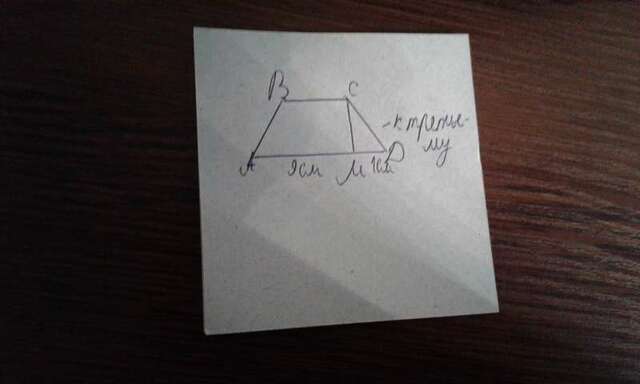
3) Равнобокая трапеция имеет свойство: высоты, проведённые с тупого угла делят противолежащее основание на два отрезка, больший из них равен полусумме оснований, а меньший отрезок полуразности оснований
Большее основание делиться на отрезки 9 см и 1 см, значит больший отрезок равен полусумме оснований и равен 9см, средняя линия также равна 9 см (по свойству)
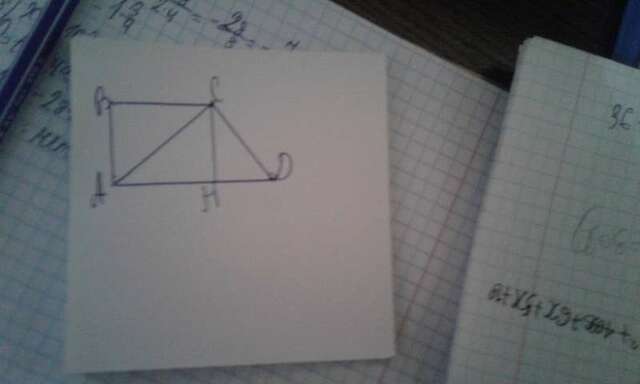
4) Проведём высоту СН с тупого угла, чтобы получить и рассмотреть прямоугольный треугольник СDH:
1) ∠D= 60° , CD= 6см, по решениям прямоугольных треугольников
DH= CD* cos 60°= 3см (катет ппямоугольного треугольника равен произведению гипотенузы на косинус прилежащего угла).
AH= 6см- 3см= 3см. Так как, ABCH - прямоугольник, то BC= AH= 3см.
5) Рассмотрим ▲BAC ∠В= 90°, ∠BAC= 45° (так как, диагональ является биссектрисой прямого угла), ∠BCA= 90°- 45°= 45°, значит треугольник равнобедренный и BC= AB= 4 см. По теореме Пифагора AC²= BC²+ AB²= 32 cм², АВ= 4√2 см. Проведём дополнительно высоту СН, она будет равна АВ, значит АВ= СН= 4 см.
В треугольнике ACН ∠D= 30°, СН= 4 см- катет. По решениям прямоугольных треугольников: CD= CH: sin 30° , CD= 4см*2 = 8см (гипотенуза павна частному от катета и синуса противолежащего угла)