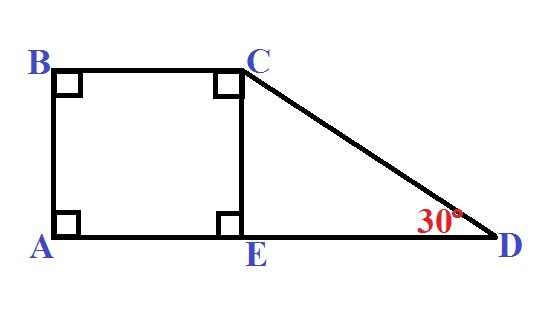
Пусть ABCD - прямоугольная трапеция.
основание AD = 14 см
основание BC = 6 cм
∠CDA = 30°
Опустим перпендикуляр (высоту трапеции) CE на основание AD.
АВСD - прямоугольник ⇒ AE = BC, AB = CE как противоположные стороны прямоугольника.
⇒ DE = AD - BC
DE = 14 - 6 = 8 (cм)
В прямоугольном треугольнике CDE
CD - гипотенуза
DE = 8 cм - катет, прилежащий к ∠СDA.
CE - катет, противолежащий ∠СDA.
Найдем СЕ c помощью тангенса ∠СDA. Тангенсом ∠CDA является отношение пртиволежащего ему катета CE к прилежащему катету DE.
CE = DE * tg(CDA)
CE = 8 * tg30° = 8 * √3/3 = 8√3 / 3 (см)
Площадь трапеции равна произведению полусуммы оснований трапеции на высоту.
AD + BC
S = --------------- * CE
2
14 + 6 8√3 10 * 8√3
S = ---------------- * --------- = --------------- = 80√3 / 3 (см²)
2 3 3