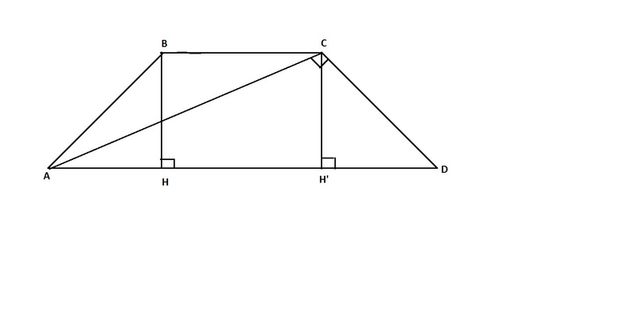
Проведём высоту BH и CH'.
BCH'H - прямоугольный (все углы прямые) ⇒ BC = HH' = 3 и BH = CH'.
AB = CD, т.к. трапеция равнобедренная
BH = CH'
∠AHB = ∠DH'C = 90°
Значит, ΔABH = ΔDCH' - по катету и гипотенузе.
Из равенства треугольников ⇒ AH = DH'.
AH + DH' = AD - BC = 5 - 3 = 2 ⇒ AH = DH' = 1.
AH' = AH + HH' = 3 + 1 = 4
В прямоугольном ΔACD CH' - высота ⇒ CH' = √AH'·H'D = √4·1 = 2 - как среднее геометрическое для проекций катетов на гипотенузу.
SABCD = 1/2(BC + AD)·CH' = 1/2(3 + 5)·2 = 8
Ответ: SABCD = 8.