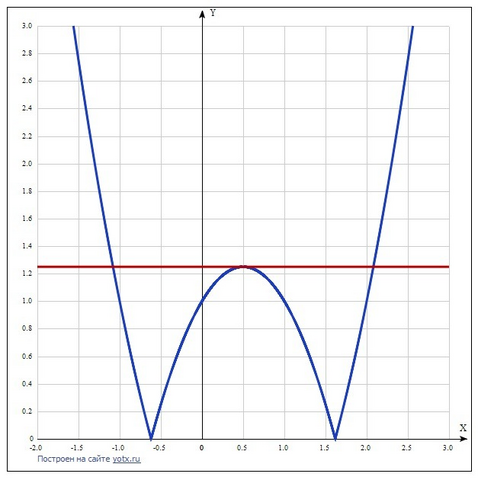
График функции у = |x^2-x-1| представляет собой параболу у = x^2-x-1, отрицательные значения которой перевёрнуты в положительную полуплоскость оси Оу. Там же будет и вершина параболы. Вот в этой точке прямая у = а и будет иметь 3 точки пересечения с графиком.
Находим абсциссу оси параболы Хо = -в/2а = -(-1)/(2*1) = 1/2.
Ордината вершины равна:
Уо = |(1/2)² - (1/2) - 1| = |(1/4) - (2/4) - (4/4)| = |-5/4| = 1,25.
Ответ: а = 1,25.