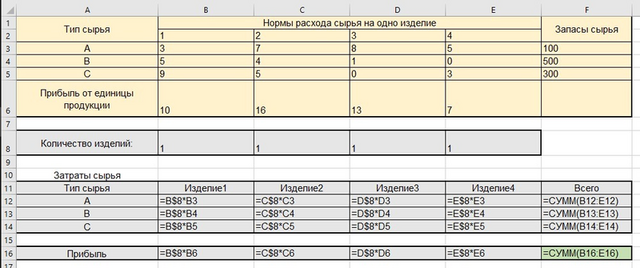
Создаём таблицу, в которую вбиваем исходные данные, а также рассчитываем для каких-то количеств продукции затраты сырья и полученную прибыль. То, что получилось у меня, показано на первой картинке.
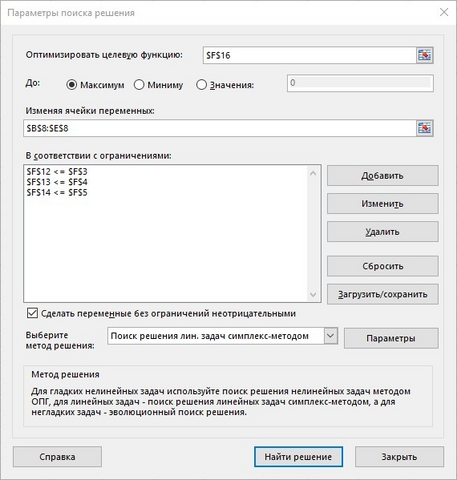
Чтобы найти решение, пользуемся "Поиском решения". В диалоговом окне необходимо указать, значение какой ячейки надо максимизировать, а также какие наложены ограничения. Так как задача линейная, у меня выбран симплекс-метод решения.
Запускаем и получаем решение.
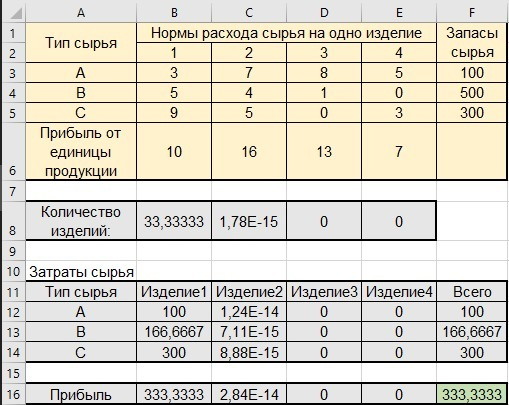
Вид таблицы для исходных данных приведен на третьей картинке. Оказалось, что выгоднее всего по максимуму производить продукцию первого типа, а все остальные не производить совсем, при этом сырьё типов А и С расходуется полностью.
Уменьшение прибыли от третьего типа продукции ничего не поменяет, ведь даже при большой прибыли производить третий тип продукции было невыгодно, при меньшей прибыли и подавно.
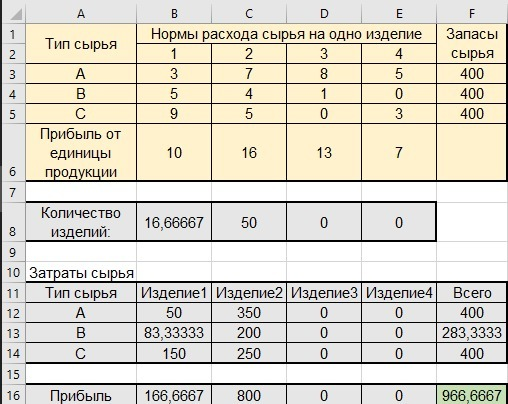
После выравнивания запасов оптимальные объёмы производства меняются, большая часть прибыли приносится продукцией 2-го типа, по-прежнему производить 3-й и 4-й типы продукции невыгодно, а ресурсы A и C в оптимальном случае выработаны полностью.