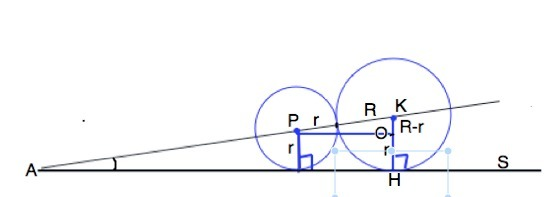
Обозначим буквой А вершину угла между прямыми РК и s. Опустим из Р и К радиусы в точки касания окружностей с прямой s.
КН=R
Проведем из Р прямую параллельно прямой s до пересечения с R в точке О.
РО║АН, АК - секущая⇒
Угол КРО=КАН– соответственные. ⇒
sin ∠KPO=1/21
В прямоугольном ∆ КОР гипотенуза РК=R+r, катет КO=R-r
sin ∠КРО=КО:РК=1/21
(R-r):(R+r)=1:21
21•(R-r)=R+r
21R-21r=R+r
20R=22r⇒
 это ответ.
это ответ.