Формула площади многоугольника, в который вписана окружность S=P•r:2
Периметр найдем из свойства описанного четырехугольника.
Четырехугольник можно описать около окружности тогда и только тогда, когда суммы его противоположных сторон равны.
Так как трапеция равнобедренная, СD=AB, и сумма боковых сторон равна 2•(4+9)=18
Значит, СВ+АD=18 ⇒ Р=36
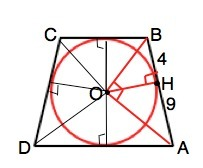
Соединим центр окружности с вершинами А и В.
Треугольник АОВ - прямоугольный, так как центр окружности, вписанной в угол, лежит на биссектрисе. ВО и АО биссектрисы.
Радиус ОН, проведенный в точку касания - высота ∆ ВОА.
Высота прямоугольного треугольника - среднее пропорциональное между отрезками, на которые она делит гипотенузу:
ОН²=ВН•АН=4•9=36
ОН=√36=6
S=36•6:2=108см*