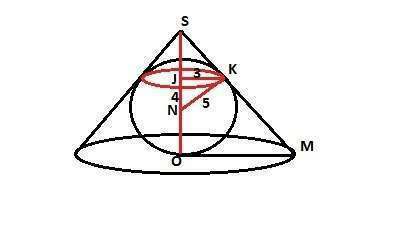
Площадь поверхности сферы:Sс=4π(Rс)² =100π, отсюда Rс=NK=5.
Длина окружности, по которой сфера касается поверхности конуса:2πr=6π, отсюда r=JK=3.
Треугольник SNK прямоугольный, так как NK -радиус в точку касания и пифагоров, так как катет=3, а гипотенуза=5.
Тогда второй катет JN=4.
JK - высота из прямого угла и по ее свойству: JK² =SJ*JN, отсюда
SJ= 9:4=2,25.
JO=JN+NO или JO=4+5=9.SО=SJ+JO или SО=2,25+9=11,25.
Треугольники JSK и OSМ подобны с коэффициентом подобия k=SJ/SO=1/5.
Тогда искомый радиус ОМ равен ОМ=JK *k или ОМ=15.
Ответ: радиус конуса равен 15.