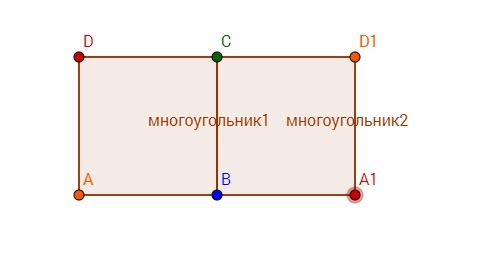
Допустим что две точки лежащие на расстоянии 1 м разного цвета,
построим квадрат со стороной 1м , тогда получим что все точки принадлежашие вершинам разного цвета.
отметим точку А1 и D1 симметричную соответственно точке А и D относительно стороны ВС ,
а так как А1 находится от точек В и D1 на расстоянии 1м она не совпадает с ними по цвету , значит она совпадает по цвету с точкой А либо С , либо D
,то есть если начертить окружность с радиусом 2 ,и центром в точке А, либо окружность с радиусом √2 с центром в точке С , либо кружность с радиусом √ 5 с центром в точке D,то все точки принадлежащие этой окружности будут одного цвета , значит найдутся две точки расстояние между которыми равно 1. .Получили противоречие.