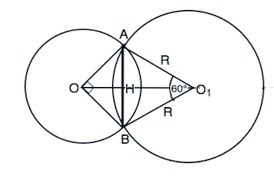
Общая хорда двух пересекающихся окружностей видна из их центров под углами 90° и 60°. Найти радиус большей окружности, если центры окружностей лежат по разные стороны от хорды, а расстояние между центрами равно 0,25(1+√3).
—————
Обозначим центр меньшей окружности О, большей - О1,
общую хорду - АВ.
ОО1 пересекает АВ в т.Н.
В ∆ АО1В угол АО1В-60°, следовательно, ∆ АО1В равносторонний и хорда АВ=АО1=R.
∆ ОАО1=∆ОВО1 - по трем сторонам.
АО=ВО, АН=ВН, ⇒ АВ⊥ОО1
О1Н=R•sin60°=R√3/2
В ∆ АОВ угол АОВ=90°
ОН - медиана ∆ АОВ и равна АВ/2=R/2 (свойство медианы прямоугольного
О1О=О1Н+НО= R√3/2+R/2=R(1+√3)/2
По условию О1О=0,25(1+√3)⇒
R(1+√3)/2=0,25(1+√3) ⇒
R=0,5 (ед. длины)