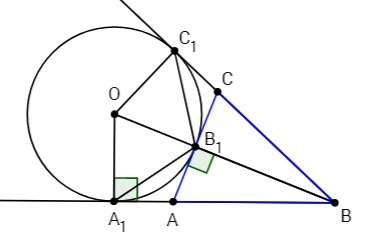
Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
△A1B1B = △C1B1B (по двум сторонам и углу)
∠A1B1B = ∠C1B1B => ∠A1B1O = ∠C1B1O (углы смежные с равными углами)
∠A1BO = ∠C1BO = 0,5∠ABC
Касательная перпендикулярна к радиусу.
∠A1OB = 90 - ∠A1BO
Центральный угол равен дуге, на которую опирается.
∠A1OB = U A1B1
Угол, образованный касательной и секущей через точку касания, равен половине дуги между его сторонами.
∠A1B1A = 0,5 U A1B1
∠A1B1O = 90 - ∠A1B1A = 90 - 0,5(90 - ∠A1BO) = 45 + 0,5 ∠A1BO
∠A1B1C1 = 2 ∠A1B1O = 90 + ∠A1BO = 90 + 0,5 ∠ABC