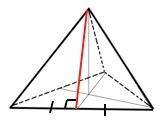
Основание правильной треугольной пирамиды - правильный треугольник Площадь полной поверхности правильной пирамиды равна сумме площади основания и площадей 3-х её граней. .
Площадь основания =S полн-S бок=72√3-60√3=12√3
Формула площади правильного треугольника


Апофемой называется высота боковой грани правильной пирамиды. Площадь боковой грани равна
S бок:3=60√3:3=20√3
S грани=h•a:2
h=2S:a=40√3:4√3=10 (см)