Идея решения такова.
1) Собираем в числителе и знаменателе полные квадраты. Получится такое:

Это равносильно системе:

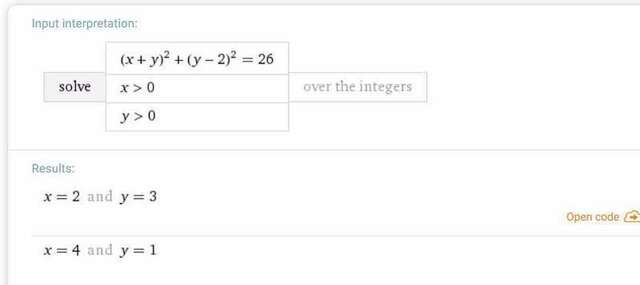
Чтобы решить первое уравнение в целых неотрицательных числах, надо понять, сумма квадратов каких двух чисел даёт 26. Очевидно, это  (других вариантов нет, можете перебрать).
(других вариантов нет, можете перебрать).
С учётом того, что под квадратом может могут быть отрицательные числа (ведь  ), у нас получится три системы линейных уравнений, которые в общем виде можно записать так:
), у нас получится три системы линейных уравнений, которые в общем виде можно записать так:

(Варианты, когда  и
и  , не рассматриваем, так как сумма двух неотрицательных чисел не может быть отрицательна.
, не рассматриваем, так как сумма двух неотрицательных чисел не может быть отрицательна.  тоже невозможно в неотрицательных числах.)
тоже невозможно в неотрицательных числах.)
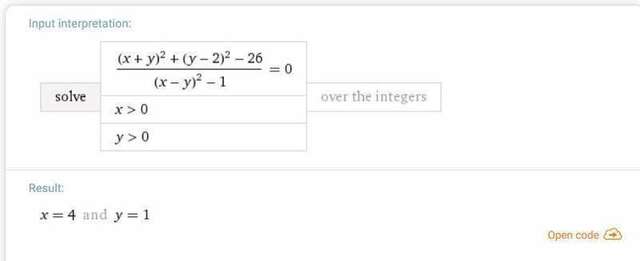
Вам остаётся только решить эти системы, а затем сверить полученные пары чисел с ОДЗ (знаменатель не равен нулю) и найти наибольшее произведение.
Все возможные решения (для проверки) см. на скриншоте (это без учёта ОДЗ).
А с учётом ОДЗ только одно решение: пара (4;1).