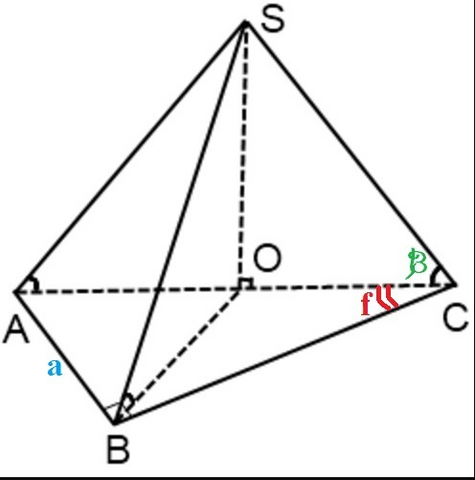
Если все боковые ребра наклонены под одним углом к основанию пирамиды, все боковые ребра равны, а вершина пирамиды проецируется в центр описанной около основания окружности. Центр окружности, описанной около прямоугольного треугольника лежит на середине гипотенузы, т.е. основанием высоты (SO) пирамиды явялется середина гипотенузы (AC) основания пирамиды.
В прямоугольном треугольнике ABC:
Катет AB = a
∠ABC = 90°
∠ACB = f
Тангенсом ∠ACB явялется отношение противолежащего ему катета AB к прилежащему катету BC.
tg(ACB) = AB / BC
BC = AB / tg(ACB)
BC = a / tg(f)
Площадь основания пирамиды SABC:
Sосн = 1/2 * AB * AC
Sосн = 1/2 * a * a / tg(f) = a² / (2tg(f))
Синусом ∠ACB является отношение противолежащего ему катета AB к гипотенузе AC
sin(ACB) = AB / AC
AC = AB / sin(ACB)
AC = a / sin(f)
CO = AC / 2 a
CO = 1/2 * a/sin(f) = --------------
2sin(f)
В прямоугольном треугольнике SOC:
Катет CO = a / (2sin(f))
∠SCO = β
SO = H пирамиды
Тангенсом ∠SCO является отношение противолежащего ему катета SO к прилежащему катету CO
tg(SCO) = SO / CO
SO = CO * tg(SCO)
SO = CO * tg β
a * tg β
SO = a / (2sin(f)) * tg β = -------------------
2sin(f)
Объем пирамиды
V = 1/3 * Sосн * H
1 a² a * tg β a³ * tg β
V = --------- * ---------------- * --------------- = ----------------------------
3 2tg(f) 2sin(f) 12 * tg(f) * sin(f)