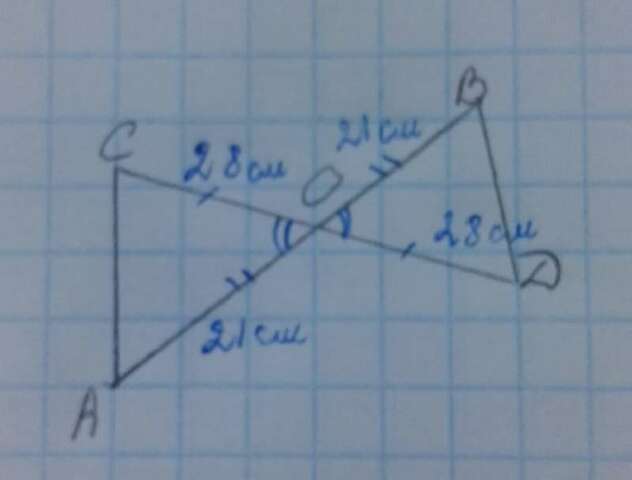
Дано: Решение:
АО = 21 см Т.к. по условию задачи
CD = 56 см отрезки АВ и CD
P = 83 см разделены т. О пополам,
Найти: то СО = 56/2 =28
BD - ? Рассмотрим
треугольники АОС и ОBD:
1) AO = OB по условию;
2)CO = OD по условию;
3)угол AOC = угол BOD, т.к. они - вертикальные.
Значит, треугольники AOC и OBD равны по двум сторонам и углу между ними.
Отсюда слудует, что периметр AOC = периметр OBD.
P OBD = OD + BD + OB
83= 28 + BD + 21
BD = 83 - 21 - 28
BD = 34 см.
Ответ: 34 см.