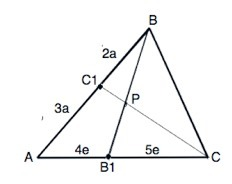
По т.Менелая: Если на сторонах AB и BВ1 треугольника ABВ1 взяты соответственно точки C1 и Р, а точка С взята на продолжении стороны AB1 за точку B1 , то точки C1, Р и С лежат на одной прямой тогда и только тогда, когда выполнено равенство:

AC=4e+5e=9e

откуда

Следовательно