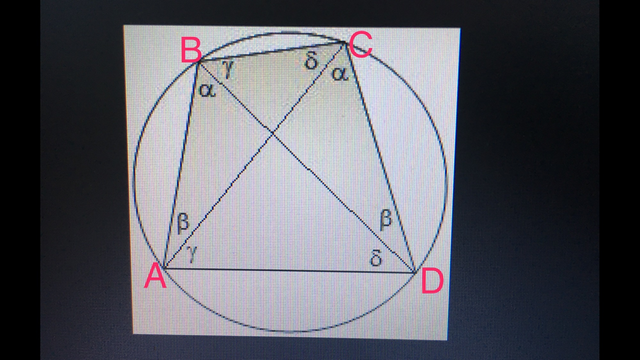
В треугольнике АВД по теореме синусов R=AD/sinα.
Также в тр-ке ACD R=AD/sinα.
1. Для треугольников АВD и ACD радиус описанной окружности одинаков, при этом они имеют общую сторону АД, значит их центры описанных окружностей совпадают, следовательно около четырёхугольника АВСD можно провести окружность.
Доказано.
2. Углы АВД и АСД лежат напротив стороны АД, значит можно сказать, что они вписанные и опираются на общую дугу АД, значит точки А, В, С и Д лежат на одной окружности, следовательно четырёхугольник АВСД - вписанный.
Доказано.