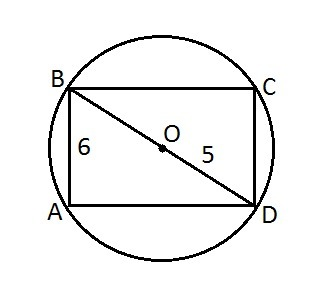
1) Пусть ABCD - прямоугольник, вписанный в окружность, АВ=6 см, R=OD=5 см.
2) Радиус описанной окружности равен половине диагонали прямоугольника: R=1/2*BD, значит диагональ BD=2*R=2*5=10 (см).
3) Рассмотрим ΔABD - прямоугольный, по т.Пифагора
AD=√(BD²-AB²)=√(10²-6²)=√(100-36)=√64=8 (см).
Ответ: 8 см.