Три окружности радиусов 2, 18, 5 касаются попарно друг друга внешним образом. Найти длину...

Question

Три окружности радиусов 2, 18, 5 касаются попарно друг друга внешним образом. Найти длину хорды, отсекаемой третьей окружностью от общей внутренней касательной первых двух окружностей.

Answer 1

Обозначим центры заданных окружностей О1, О2 и О3.
Начало координат примем в точке О1(0; 0).
О2(20; 0). Здесь 20 = 2+18.
Координаты центра третьей окружности надо решить из системы двух окружностей (как построение треугольника).


Из второго уравнения вычитаем первое и получаем:
-40х + 400 = 480  или х - 10  = -12.
Отсюда х = -12 + 10 = -2.
у = √(49-4) = √45 = 3√5.  Это координаты точки О3.
Уравнение третьей окружности: (х + 2)² + (у - 3√5)² = 25.
Общая касательная к первой и второй окружностям имеет уравнение:
х = 2.
Подставим х = 2 в уравнение третьей окружности и найдём координаты точек пересечения общей касательной двух окружностей с третьей окружностью.
(2+2)²+(у-3√5)² = 25.
16 + у² - 6√5*у +45 = 25.
Получаем квадратное уравнение:
у² - 6√5*у + 36 = 0.
Квадратное уравнение, решаем относительно y: Ищем дискриминант:
D=(-6*2root5)^2-4*1*36=36*5-4*36=180-4*36=180-144=36;Дискриминант больше 0, уравнение имеет 2 корня:
y_1=(√36-(-6*√5))/(2*1)=(6-(-6*√5))/2=(6+6*√5)/2=6/2+6*√5/2=3+6*√5/2=3+3*√5≈9.7082039;y_2=(-√36-(-6*√5))/(2*1)=(-6-(-6*√5))/2=(-6+6*√5)/2=-6/2+6*√5/2=-3+6*√5/2=-3+3*√5≈3.7082039.
Разность координат по оси Ох равна 6.
Это и есть длина искомой хорды.

Answer 2

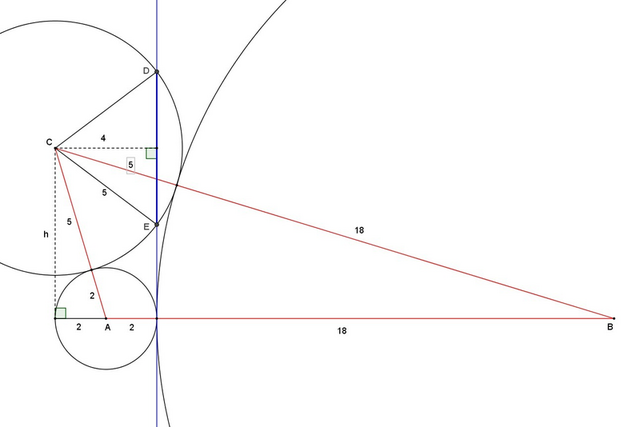
Будем считать, что окружности пронумерованы в порядке их перечисления в условии, а А, В, С - соответственно их центры. 
AB=2+18=20, AC=2+5=7, BC=18+5=23.  По ф. Герона p=(20+7+23)/2=25
S(ABC)=√(25·5·18·2)=30√5. Расстояние h от точки С до прямой AB равно h=2S/AB=3√5. Расстояние от С до  общей внутренней касательной к окр. А и В равно 2+√(AC²-h²)=2+√(49-45)=4. Значит искомая хорда DE равна 2√(5²-4²)=6.

---