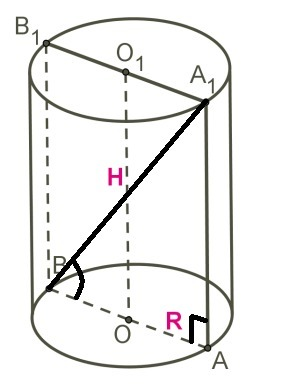
Осевым сечением цилиндра является прямоугольник ABB1A1.
В прямоугольном треугольнике A1AB:
∠A1AB = 90°
∠ABA1 = 60°
∠AA1B = 180 - 90 - 60 = 30 (°)
⇒ катет АВ, противолежащий углу 30°, равен половине гипотенузы A1B.
AB = A1B / 2
AB = 16 / 2 = 8 (cм)
AB является диаметром окружности основания цилиндра
⇒ AB = 2R
R = AB / 2
R = 8 / 2 = 4 (cм)