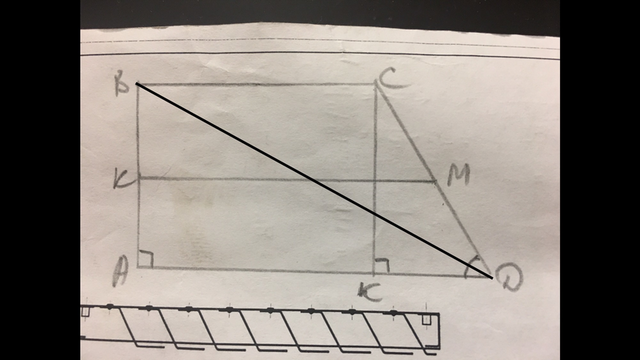
В трапеции АВСД АД║ВС, АВ⊥АД, АД=18 см, СД=10 см, ∠АДВ=∠СДВ.
В трапеции биссектриса отсекает от противолежащего основания (или его продолжения) отрезок, равный прилежащей боковой стороне (свойство трапеции). ВД - биссектриса угла Д, значит ВС=СД=10 см.
Опустим высоту СК⊥АД.
КД=АД-АК=АД-ВС=18-10=8 см.
В треугольнике СДК СК²=СД²-КД²=10²-8²=36,
СК=6 см.
S=h(a+b)/2=СК(АД+ВС)/2=6(18+10)/2=84 см² - это ответ.