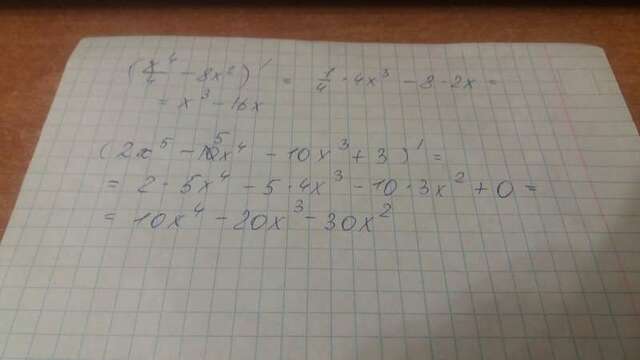Находим производные обеих функций и приравниваем их к нулю
1) производная: 2) производная:
x^3 - 16x 10x^4 - 20x^3 - 30x^2
x^3 - 16x = 0 10x^4 - 20x^3 - 30x^2 = 0 | :10
x(x^2 -16) = 0 x^4 - 2x^3 - 3x^2 = 0
x = 0, x = 4, x =-4 x^2(x^2 - 2x -3) = 0
-4 и 4 не принадлежат x = 0, x = -1, x = 3
отрезку [ -1 ; 2 ] 3 не принадлежит отрезку [ -2 ; 2 ]
подставляем -1, 0 и 2 в функцию подставляем -2, 0 ,-1, 2 в функцию
y(-1) = 0.25 - 8 = -7.75 y(-2)= -64+80+80+3 = 99
y(0) = 0 y(0) = 3
y(2) = 4 - 32 = -28 y(-1) = -2+5+10+3 = 16
y(2) = 64 + 80 - 80 + 3 = 67
y(min) = -28 y(min) = 3
y(max) = 0 y(max) = 99