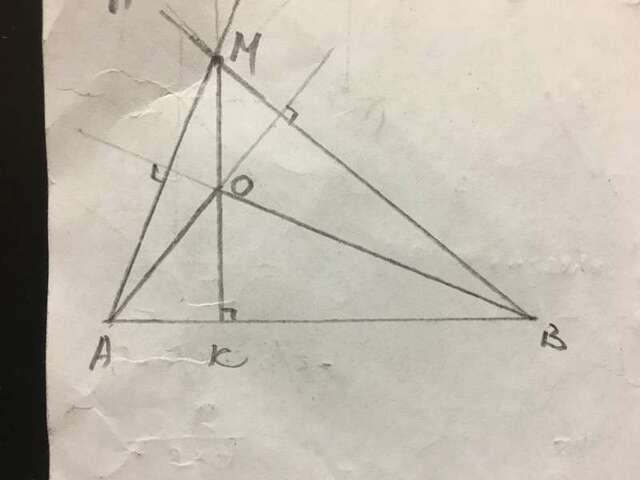
Высота треугольника пересекаются в одной точке, называемой отроцентром треугольника, значит высота ОК, проведённая к стороне АВ, проходит через точку М, следовательно МО⊥АВ.
В треугольнике АМО высота, проведённая к стороне МО равна АК, а в треугольнике ВМО такая же высота равна ВК.
S(АМО)=МО·АК/2=25·АК/2=12.5АК,
S(ВМО)=МО·ВК/2=12.5ВК.
S(АОВМ)=S(АМО)+S(ВМО)=12.5(АК+ВК)=12.5АВ=12.5·60=750 мм² - это ответ.
-------------------------------
Можно рассмотреть четырёхугольник АОВМ. В нём МО и АВ - диагонали, они перпендикулярны. S(АОВМ)=(d1·d2·sinα)/2=(MO·AB·sin90)/2=25·60·1/2=750 мм².