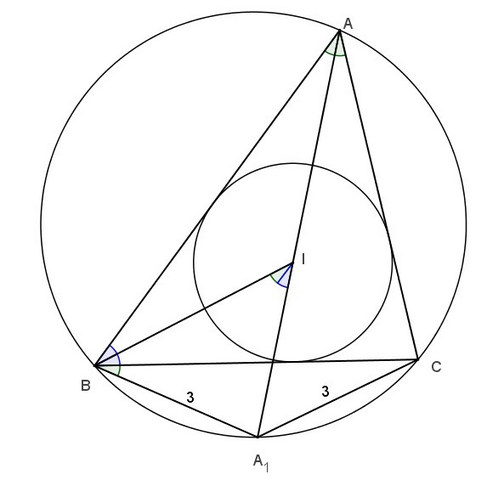
Т.к. ∠BAA₁=∠CAA₁ и являются вписанными, то они опираются на равные хорды, т.е. A₁B=A₁C=3.
I - точка пересечения биссектрис треугольника ABC.
∠BIA₁=∠A/2+∠B/2 как внешний угол треугольника ABI.
∠IBA₁=∠CBA₁+∠CBI=∠A/2+∠B/2, т.к. ∠CBA₁=∠CAA₁=∠A/2 как вписанные.
Значит ∠BIA₁=∠IBA₁, т.е. треугольник BIA₁ - равнобедренный и A₁I=A₁B=A₁С=3. Итак, A₁I+A₁B=6.
Значение стороны АВ оказалось не нужным для решения.