Треугольник вписан в окружность.
АС - радиус описанной окружности, ВС - сторона треугольника, ВD - медиана.
Построить треугольник.
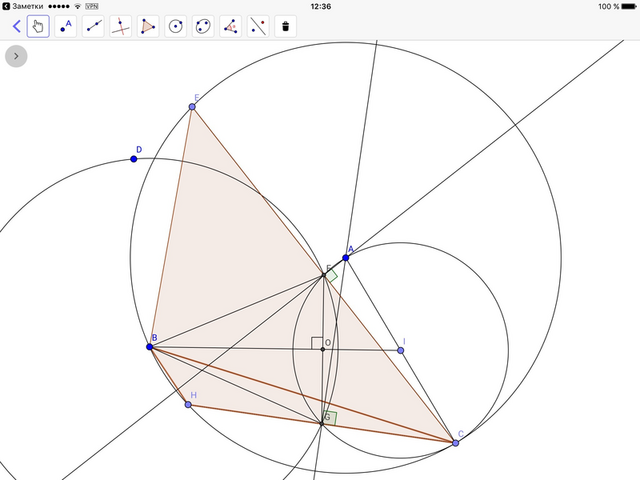
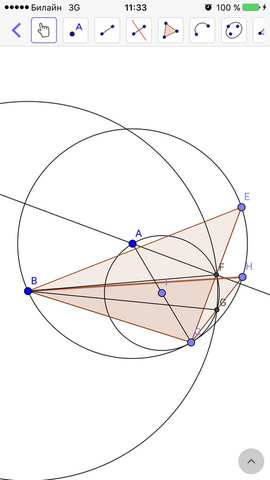
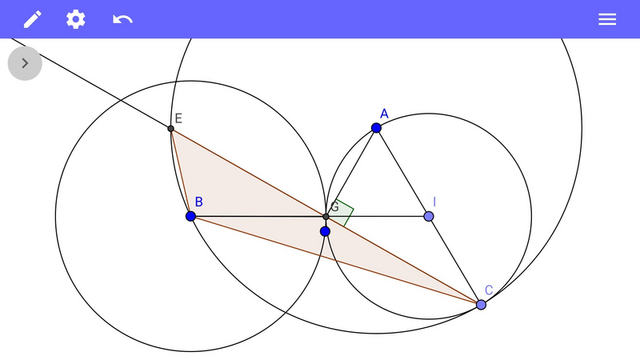
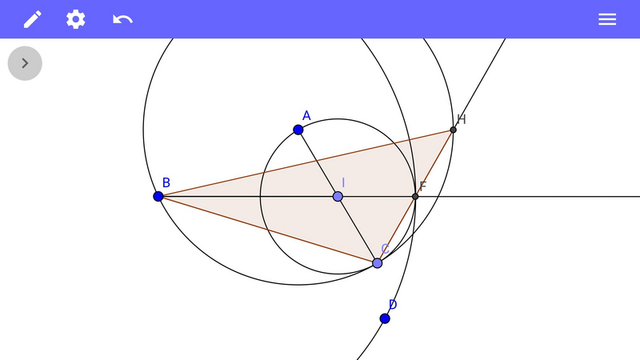
Построим окружность с радиусом АС и сторону треугольника ВС в виде хорды.
Из точки В построим окружность с радиусом, равным медиане ВD.
Из середины отрезка АС построим окружность диаметром АС. Точка I - центр этой окружности.
Две последние окружности пересекаются в точках F и G.
BF=BG=BD - отрезки, равные данной медиане.
Из точки С через точки F и G построим хорды СЕ и СН.
Вписанные треугольники АСF и АСG прямоугольные так как опираются на диаметр АС, значит отрезки AF и AG перпендикулярны хордам СЕ и СН. Точка А - центр окружности для эти хорд, значит CF=EF и CG=HG.
Получилось два треугольника СВЕ и СВН, удовлетворяющие условию задачи.
Рассматривая варианты построения можно заметить, что при данных стороне и радиусе описанной окружности построить можно только тот треугольник, у которого длина медианы позволяет окружностям с центрами в точках В и I пересечься.
Если же получилось, что медиана лежит на отрезке ВI, то треугольник получится только один так как окружности с центрами В и I будут лишь касаться.
Предлагаю варианты построения для постоянных длин стороны АС и радиуса описанной окружности АС. Меняется только длина медианы ВD.