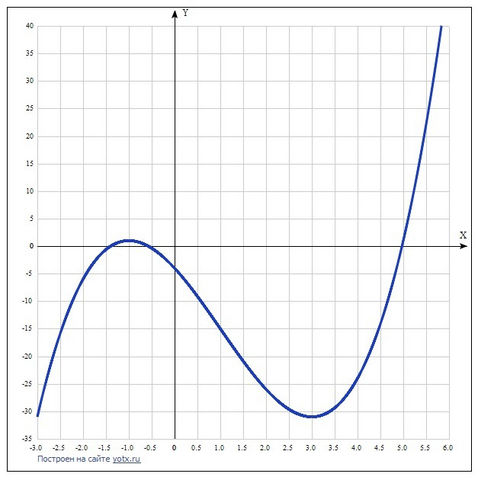
Производная функции f(x)=x^3-3x^2-9x-4 равна:
f '(x) = 3x² - 6x - 9.
Приравниваем её нулю:
3x² - 6x - 9 = 0,
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=(-6)^2-4*3*(-9)=36-4*3*(-9)=36-12*(-9)=36-(-12*9)=36-(-108)=36+108=144;Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√144-(-6))/(2*3)=(12-(-6))/(2*3)=(12+6)/(2*3)=18/(2*3)=18/6=3;x_2=(-√144-(-6))/(2*3)=(-12-(-6))/(2*3)=(-12+6)/(2*3)=-6/(2*3)=-6/6=-1.
Значит, экстремумы в точках:
(-1, 1),
(3, -31).
Минимум функции в точке: x = 3.
Максимум функции в точке: x = -1.
Возрастает на промежутках (-oo, -1] U [3, oo).
Убывает на промежутке [-1, 3].