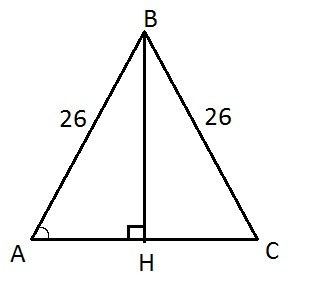
1) Пусть ΔАВС - равнобедренный, АВ=ВС=26 см, cosA=cosC=5/13, ВН - медиана.
2) Рассмотрим ΔАНВ - прямоугольный, так как медиана в равнобедренном треугольнике, проведенная к основанию, является и высотой и биссектрисой.
cosA=AH/AB=5/13;
AH/26=5/13;
AH=26*5/13=10 (см).
3) По т.Пифагора находим медиану ВН=√(АВ²-АН²)=
=√(26²-10²)=√(676-100)=√576=24 (см).
4) Рассмотрим ΔАВС: АН=1/2*АС, АС=2*АН=2*10=20 (см).
Ответ: 20 см, 24 см.