Общая схема исследования функции. 1.​ Найти область определения и область значения...

0 голосов
41 просмотров

Общая схема исследования функции.

1.​ Найти область определения и область значения функции.

2.​ Исследовать функцию на четность-нечетность.

3.​ Найти вертикальные асимптоты.

4.​ исследовать поведение функции на бесконечности, найти горизонтальные или наклонные асимптоты.

5.​ Найти экстремумы функции и интервалы монотонности функции.

6.​ Найти интервалы выпуклости (вогнутости) и точки перегиба.

7.​ Найти точки пересечения графика с осями координат и, возможно, некоторые дополнительные точки, уточняющие график.

y=(2+x^2)e^x^2

Математика (20 баллов) | 41 просмотров
Дан 1 ответ
0 голосов
Правильный ответ
y = (2 + x^2)*e^{x^2}
1) Область определения: (-oo; +oo).
2) Четная, непериодическая.
3) Вертикальных асимптот нет.
4) На бесконечности
\lim_{x \to +-\infty} (2 + x^2)*e^{x^2}=(2+\infty)*e^{+\infty}=+\infty
Наклонные и горизонтальные асимптоты
f(x) = kx + b
k = \lim_{x \to \infty} \frac{y(x)}{x} = \frac{(2 + x^2)*e^{x^2}}{x}=+ \infty
Асимптот нет.
5) Экстремумы
y'=2x*e^{x^2}+(2+x^2)*e^{x^2}*2x=2x*e^{x^2}(3+x^2)=0
x = 0; y(0) = (2 + 0)*e^0 = 2*1 = 2 - точка минимума.
При x < 0 будет y' < 0 - функция убывает.
При x > 0 будет y' > 0 - функция возрастает.
6) Область значений функции: [2; +oo)
7) Точки перегиба
y'=2x*e^{x^2}+(2+x^2)*e^{x^2}*2x=(6x+2x^3)*e^{x^2}
y''=(6+6x^2)e^{x^2}+(6x+2x^3)e^{x^2}*2x=(6+18x^2+4x^4)e^{x^2}=0
4x^4 + 18x^2 + 6 = 0
Биквадратное уравнение, делим все на 2
2x^4 + 9x^2 + 3 = 0
D = 9^2 - 4*2*3 = 81 - 24 = 57
x1^2 = (-9 - √57)/4 < 0 - не подходит.
x2^2 = (-9 + √57)/4 < 0 - не подходит.
Точек перегиба нет. При любом х будет y'' > 0.
График везде выпуклый вниз (вогнутый).
8) Точки пересечения с осями.
y(0) = 2, это мы уже вычислили.
y ≠ 0 ни при каком x, пересечений с осью абсцисс нет.
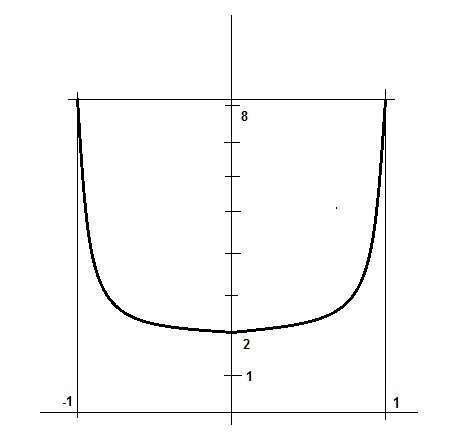
y(-1) = y(1) = (2 + 1)*e^1 = 3e ~ 8,15
Точный график мелкий и примерный, но крупный - на рисунках.
image
image
(320k баллов)
Похожие задачи